F1、F2、どちらが大きな荷重がかかるか分かりますか? 次の計算式で求めます。

【モーメント】と【力のつり合い】
【モーメント】と【力のつり合い】は次の公式になります。※ブラケットの自重は加味しないとします。
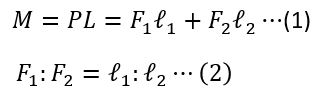
荷重F1とF2の算出


正解は
F2 でした。あとはボルトにかかる引張応力と安全率を計算して強度を満足するか確認しましょう。
ボルトがその強度に耐えられない場合、単純にボルト本数を増やすことですぐに解決できますが計算が少々手間になります。そこでボルト本数がN本以上の場合の計算については下記記事で紹介していますので参考になればと思います。
また、実際にボルトでブラケットを固定する際に必要な締付トルクはどの程度が良いか、トルクレンチでの締付によるトルク計算方法も紹介しています。非常に面倒なパラメータ情報調査を省くために情報を一覧化した表を作成しました。参考になればと思います。
さらに、もっと簡単にブラケットを設計するための材質や形鋼のシンプルな選定方法について下記記事で紹介しています。
まとめ
このような簡単設計でも計算しておくと安心感が得られます。簡単な設計だからこそ応急的な対応で求められることが多く、その際に関数を組み込んだエクセルシートを持っておくと効率的に対応することができます。
関数を組み込んだエクセルをダウンロードできるようになりました。当ブログメニューしんめ倉庫参照
参考情報
材質について機械的性質や海外規格とあわせて一覧表にしました。参考までに。






コメント
ボルト2本分の荷重を仮想モーメント中心からの長さの比で計算するのはどのような考え方に基づくものでしょうか?
例えば今回の条件では、仮想モーメント中心を図の下端の、F1下部からの比として計算してますが、仮に仮想モーメント中心をL字の折れ曲がった根本部分で考えた場合、おそらく長さの比が異なってしまい、ボルト荷重が変化してしまうような気がします。
コメントありがとうございます。
◆なぜ仮想モーメント中心を“図の下端(F1下部)”に設定しているのか?
結論から言うと、経験則と破損傾向の観察に基づいています。
設計および現場での確認経験から、片持ちブラケットの破断・緩み・脱落の多くは上側のボルトで発生しています。
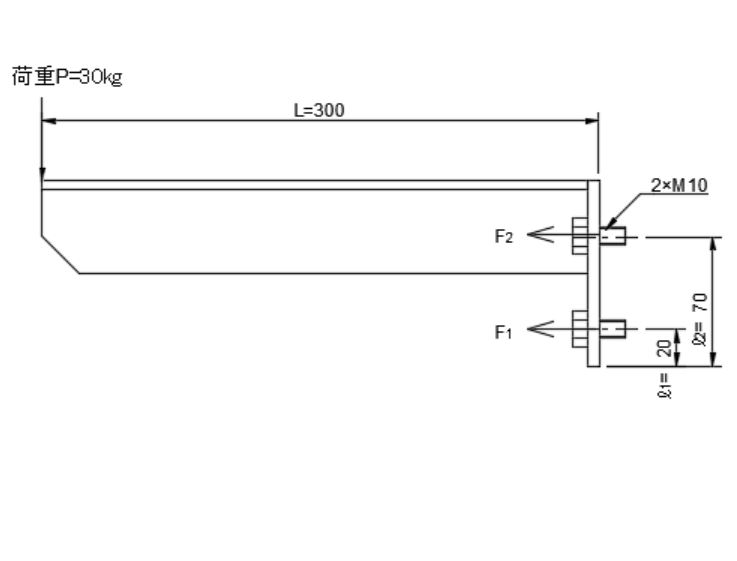
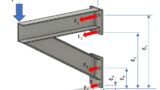
また、下図のように取付面を強力な両面テープで模擬し、ブラケット先端に荷重 F を加えると、片持ち荷重により反時計回りのモーメント(M = F・L) が生じます。
このとき接触面の圧力分布は、下端側が圧縮支点、上端側が引張(開き) となる三角分布に近づきます。
そのため、最初に間隙が生じ=剥離が始まるのは上端です。
この「圧縮側の縁(下端)を支点とみなす」考え方が、本文で用いている仮想モーメント中心です。
したがって、ボルトの引張荷重はこの仮想中心(下端)からの距離比に概ね比例して分担され、上側ボルトほど大きな引張力を受けます。
◆“L字ブラケットの根本”を中心と考えた場合、結果が変わらないか?
ご指摘のとおり、仮想モーメント中心の位置をどこに取るかによって、ボルト荷重の比は変化します。
仮想モーメント中心は理論的には「接触面の反力分布とボルトの引張力が釣り合う位置」として定義され、
これはブラケットの剛性分布や取付条件によって変化し得るものです。
当ブログでは、実際の挙動と経験的傾向を重視し、簡易的に「ブラケット下端」を仮想モーメント中心として計算しています。